数の概念を理解（獲得）する年齢は？足し算・引き算ができるのはいつから？ - 言語聴覚士は放課後等デイサービスで何ができる？

数の概念と計算

よく「この子は１０まで言えるから、１～１０までの数の理解をしています」という話しを聞きます。言えること＝理解しているなのでしょうか？

また、足し算、引き算などの計算ができるまでにはどんな力が必要なのでしょうか？

今回は、数の理解と、加減算の獲得までの流れについてです。

数の概念と計算
- 足し算と引き算ができるようになる年齢
頭のなかだけで考えるものではない
- 獲得する目安
- 数の概念を理解するために
数を数えるために必要なルール（計数原理）
- 加減算の基礎となる計数の発達
- 数を理解する
まとめとして

足し算と引き算ができるようになる年齢

結論から言うと・・・

計算ができるようになる年齢

・足し算　5歳
・引き算　6歳

もちろん、かんたんな計算のみです。

それ以前にできはじめる子もいます。

計算ができるイコール数の概念を理解しているわけではありません。

概念を理解するためには前提となる力を身につける必要があるのです。

それでは、その「前提となる力」を段階でみていきましょう。

頭のなかだけで考えるものではない

数は頭の中だけで考えるものではありません。頭だけではなくて、手や指を使ったり、目で見たり。運動しながら考えるものです。数も自分の身体が基本です。

●声と手の動き（運動）

数を数える時、「いち、に、さん」という声と対象を指さす指の動きが合っていることが必要。

●目と手の動き（運動）

端から順に間を飛ばさずに数えること

複数の感覚を一緒に使っているということがポイントです。

獲得する目安

①第１段階（～３歳）

数を機械的に覚えているだけ。数を使って物を考えられない

②第２段階（３、４歳～）

・数を見聞きして多少を判断する
・数字を読む
・おはじきを取りだす

※確実に操作できるのは９以下

③第３段階（５歳～）

・操作できる数が１０以上まで拡がる
・数唱は２０まで
・物の数を数える（１０まで）
・１０まで数字が読める
・答えが５以下になる加算（足し算）

④第４段階（６歳～）

・１１～１９までの数字を読める
・１３個の物を数えられる
・複数の中から１２個だけ取り出せる
・簡単な引き算（減算）ができる
・１０以内の数を逆から言えるようになり始める（逆唱）

繰り上がりの計算は小学校就学後～

数の概念を理解するために

数のルールに気づくことが大切です。

数には大きく分けると２つの意味があります。

① 順序

　⇒ 数は「１，２，３・・・」と順番を表している

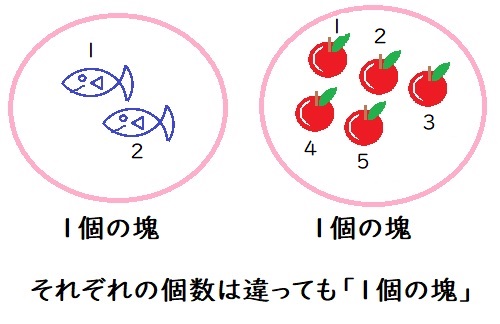
② 集合

　⇒ 数がいくつでも塊となれば「１個の塊」となる

これらを理解するためにに「計数」というルールを身につけることが大切です。

数を数えるために必要なルール（計数原理）

理解して数を使うためには「計数のルール」を身につけることが必要です。

計数とは、数をかぞえる＆計算をするということ

この計数を身につけるためには５つの原理が必要であるとゲルマン（アメリカの心理学者）は言っています。

ゲルマン 5原則

① １対１対応の原理
② 順序無関係の原理
③ 安定順序の原理
④ 基数の原理
⑤ 抽象の原理

①数を数えるときには、１つの物に対して１回しか数えない。（１対１対応の原理）

⇒ これが理解できないと「今から数えるもの」と「既に数え終えたもの」がゴチャゴチャになってしまいカウントできません。

②どれから数えても総数は変わらない。（順序無関係の原理）

③数の並びはいつでも同じ。（安定順序の原理）

⇒ 物を数えるとき、「１、２、３、４、５・・・」という並び方は変わることはないということです。

④あるものの数を数えたとき、一番最後に行った数が前他の大きさを表す。（基数の原理）

⇒ 「１、２、３、４、５」とすべてを数え終えたら、この集合体の総数は「５個」ということになります。

⑤大きくても小さくてもそれぞれ１とカウントする（抽象の原理）

⇒ 「白い車×２、赤い車×１、黒い車×２、車は合計５台」
「赤ちゃん×１、お姉さん×２、お爺さん×１、人は合計４人」
何を数えても１は１。数え方は一緒ということです。

加減算の基礎となる計数の発達

数を数えるためは「計数」が必要だということが分かりました。

それでは、足し算（加算）や引き算（減算）ができるためにはどんな力が必要なのでしょうか？

１から１０まで順番に数えることができても
指定された数で止めることができない
自分が知っている数までカウントしてしまう

↓

指定された数で止めることができるようになると
加算（足し算）ができるようになってくる

また「１０，９，８・・・」のように、逆から数を言えるようになってくる（逆唱）
これで減算（引き算）も出来るようになってきます。

もう一つ大切なのが「記憶」する力です。これがうまくいかないと計算はできません。

●視覚と記憶

「１＋２＝３」
→ 視覚と記憶で対応できる

「１個にあと２個を合わせたらいくつ？」
→ ことばでイメージを浮かべて対応する

ex.「２＋３」のような文章題の可算が出来るには
・５まで読める
・５個の物を数えられる
・１０まで言うことができる（数唱）
・４と２の多少が分かる

数を理解する

● 数のルールに気づく

① 順序

数は「１，２，３・・・」と順番を表している

② 集合
数がいくつでも塊となれば「１個の塊」となる

● 計数

①数を数えるときには、１つの物に対して１回しか数えない。（１対１対応の原理）
②どれから数えても総数は変わらない。（順序無関係の原理）
③数の並びはいつでも同じ。（安定順序の原理）
④あるものの数を数えたとき、一番最後に行った数が前他の大きさを表す。（基数の原理）
⑤大きくても小さくてもそれぞれ１とカウントする（抽象の原理）

その他にも

・数の意味に気づく
「いち、に、さん」という数字と「１個、２本、３番目」などの数詞が対応することに気づく

・物を数える

・数を言うことができる

・分割でいうことができる
「１，２，３・・・１０」ではなく「４、５，６・・・１０」と途中から数えられる

・分割を逆から言える
「１０，９，８・・・１」ではなく「５，４，３・・・１」と途中から逆に言える

・多少の判断ができる
「９を２はどちらが多いか」が分かる